Whitening, three ways

Efficient coding of natural image statistics in the retina

Silicon retina response to a moving soccer ball. Mahowald and Mead 1991.

On the way to the cortex, information from photoreceptors must go through at least two bottlenecks: 1) the conversion from an analog signal to spikes (discussed last time)¹, and 2) the optic nerve, which has fewer fibers than the retina has photoreceptors. Analogous to how digital images are encoded to save memory and bandwidth, visual information must also be compressed. This is possible because of redundancies in the signals.

The statistics of natural scenes are quite consistent. If you measure the correlation of grayscale pixel values as a function of spatial distance, pixels that are close together look more similar on average. This makes sense, as they are likely part of the same object or texture.

Because of these correlations, you can imagine that it would be wasteful to have a wire from each photoreceptor down the optic nerve that conveys simply the value at a location. The plot above tells us that given a photoreceptor’s response, you’d already know a fair amount about the responses of neighboring cones.

If we look in the frequency domain, there is another type of correlation: the power spectrum of natural images drops off at a rate of 1/f². Each trace below is a different image, obtained by averaging over orientations. A decorrelated power spectrum would be flat, which is the signature of white noise.

The power spectrum of natural images falls off as 1/f². Each trace corresponds to a different image, averaged across orientations. Field 1987.

We will illustrate the concept of redundancy reduction by defining whitening, how it’s implemented in the retina, and how it’s been implemented in silicon. These three ways also coincide with the principles of the course outlined at the beginning: mathematical explanations, observations from nature, and how to build a brain.

Theoretical

Suppose you have a 10x10 pixel image. You could plot the image as a point in a 100-dimensional space. Personally, I cannot visualize 100 dimensions, but we can simplify this to a hypothetical 2-pixel “image”, and plot in 2D such that each point with coordinates (x,y) in the plots below represents an image. Across the original images, there are redundancies. For example, looking at the leftmost plot, just knowing that a point has x=2 tells you something about y: it is likely between 0 and 2. Other points with x≈2 probably also have similar y values. In the rightmost plot, we now represent the same data transformed such that the y corresponding to x=2 is evenly distributed around 0. Knowing x does not give you much information about y, or about other points with x≈2. We call this decorrelated and independent.

Whitening applied to a set of 2-pixel “images”. Orange and green points chosen to demonstrate the change to an individual point across whitening steps. X=data, E=eigenvectors of the covariance matrix, Λ^-1/2=diagonal scaling matrix.

Here are the whitening steps:

1. Decorrelate: take the eigenvectors of the covariance matrix of the data, and project the data onto these eigenvectors. This amounts to rotating the data such that its main axes are the ones of highest variance.

2. Sphere/whiten: equalize the variance in all directions (divide by the standard deviation) such that the distribution is decorrelated and independent. This is called whitening because if you think of the eigenvector decomposition as a frequency analysis, we’re equalizing power in all directions (which would result in flat power spectra in the earlier plot).

3. Rotate: rotate back to the original orientation to calculate weighted combinations in pixel space.

We can concatenate these linear operations into one matrix W, and plot each weight over the image distribution.

\(W = E\Lambda ^{-\frac{1}{2}}E^\top\)

The first weight vector W1 transforms a point (x,y) by calculating a weighted difference between x and y (positive x, negative y). W2 does some amount of y-x². In 2D, it’s hard to understand what this means beyond the operations. Let’s look at 10x10 natural images: W ends up looking like a set of center-surround filters.

This is a generalized version of the 2D case. Each filter is saying: take some positive amount of one pixel, a negative amount of the pixels around it, and sum those together. Rather than conveying the value at each pixel, which would contain redundancies, it performs a local difference operation. After applying these types of filters, what do actual whitened images look like?

Top: raw images, bottom: whitened. Images from David Field.

Yay! We hypothesize that this more or less approximates signals being sent down the optic nerve. But how does the retina do this?

Empirical

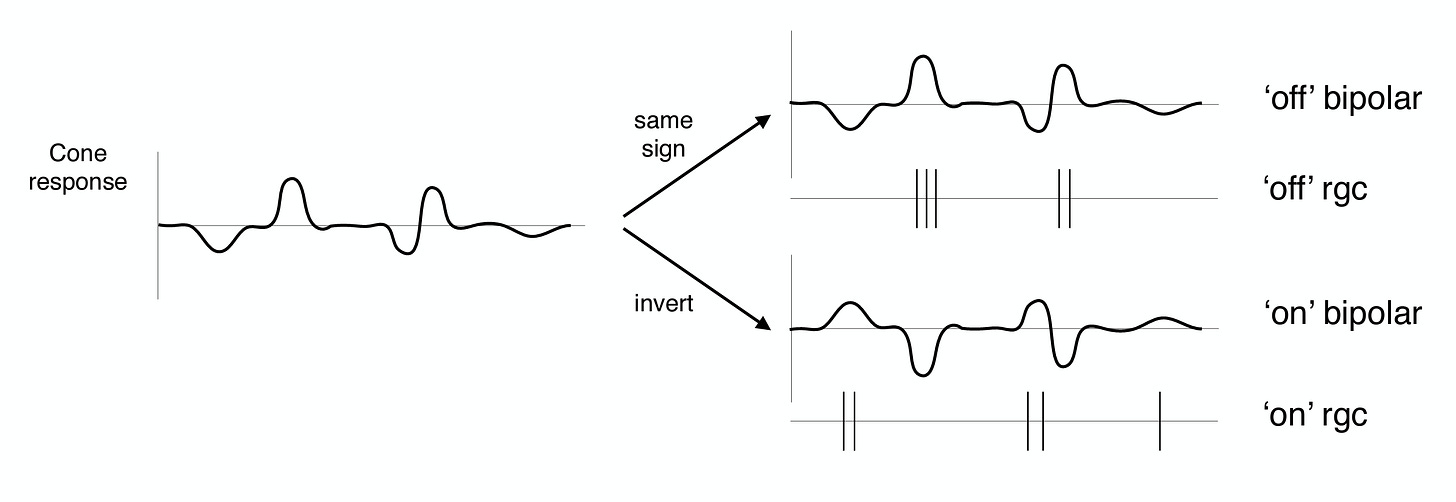
For a cone in the fovea (the highest resolution part of the retina), there are corresponding “on” and “off” bipolar and retinal ganglion cells (RGCs send information down the optic nerve). They respond to deviations from the mean in the positive and negative direction, as in the schematic below.

Horizontal cells pool over groups of photoreceptors, and serve to inhibit photoreceptor activity relative to the local population. Combined with bipolar cells that drive the center of the receptive field, this gives rise to center-surround RGC receptive fields. These localized filters are also easily wired by the connections between photoreceptors, bipolar cells, horizontal cells, and RGCs.

Remarkably, we can arrive at the same whitening solution through another approach. Karklin & Simoncelli 2012 derive whitening filters by optimizing an objective function: maximize the mutual information between the input and the activity (first term) while penalizing unit activity (second term). X is a set of images, R is RGC firing rates. λ is a weight term that indicates how strongly to penalize activity, and the brackets indicate averaging over images.

\(I(X;R) - \sum_j \lambda_j \langle r_j \rangle\)

The model is constructed as follows: to get a firing rate rᵢ, take an inner product of an image with the wᵢ, pass it through a nonlinearity fᵢ that forces values (firing rates) to be non-negative, and add some noise nᵢ.

Karklin & Simoncelli 2012.

If the goal were just to compress the image, W could be any set of independent filters. But with the extra conditions — 1) non-negative firing rates, 2) the noise floor pushing firing rates up³, and 3) the penalty pushing firing rates down — we end up with the center-surround filters below.

Left: filters W learned by the model, where dark are OFF- and light are ON-center. Middle, right: overlaid spatial envelopes of the filters show that they roughly tile the space. Karklin & Simoncelli 2012.

There is nothing in the model or optimization that explicitly says to whiten or use localized filters; they emerge from the imposed constraints, trained on natural images. When multiple approaches converge to the same answer, it’s usually a good sign. Statistical, biological, and information-theoretic methods all seem to arrive at this whitening solution!

Synthetic

Other than the retina itself, everything we’ve seen so far is a simulation of whitening, implemented on digital machines. Modern computing architecture is predicated on performing operations without error, with physical constraints abstracted away. But imposing digital precision on an inherently imprecise analog signal is costly. Misha Mahowald and Carver Mead, the inventors of the silicon retina, estimated (in 1991) that

the most efficient digital integrated circuits envisioned will consume about 10^-9 joule per operation, whereas neurons expend only 10^-16 joule. In digital systems, data and computational operations must be converted into binary code, a process that requires about 10,000 digital voltage changes per operation. Analog devices carry out the same operation in one step and so decrease the power consumption of silicon circuits by a factor of about 10,000⁴.

To build a retina, they construct a hexagonal grid of pixels where each pixel has analogues of a photoreceptor, horizontal cell connections, and a bipolar cell. The key is that each pixel performs a difference operation between the photoreceptor input⁵ and the circuit average at that location: the resistor network (horizontal connections) calculates the local average voltage, and the amplifier (bipolar cell) outputs the local difference. The voltage at each pixel represents a spatially-weighted average of photoreceptor inputs, where the weighting decays exponentially with distance, like in a network of real neurons modeled by a cable equation. Beautifully, the response of this synthetic retina approximates the human retina (local difference = center-surround AKA whitening), and all of these computations are done at low power, with physics!

The hexagonal grid of pixels of the silicon retina. In the circle: a photoreceptor P drives the resistive network with conductance G; an amplifier (“bipolar cell”) takes the difference between the photoreceptor output and the voltage on the network; six resistors and a capacitor C (“horizontal connections”) connect each pixel to its neighbors. Mead and Mahowald 1988.

For more details, see Chapter 15 of Analog VLSI and Neural Systems.

Phew, this post got way longer than I expected. I think you’d need at least a month to do this topic justice. Sadly, I have some deadlines coming up, and I’ll need to pause the lecture posts for a couple of weeks. We will resume with types of representation learning and their limitations.

1. This is estimated to be about 300 bits/sec photoreceptors and bipolar cells to 1-3 bits/spike in RGCs.

2. Note that unlike principal components analysis, the weights are not the direction of highest variance.

3. Decreasing the noise results in more oriented, less localized filters.

Karklin & Simoncelli 2012.

4. The Silicon Retina, Mahowald and Mead (1991).

5. The photoreceptors respond logarithmically in light intensity, allowing higher dynamic range and calculation of intensity ratios (subtraction in logarithmic space).