Neural nonlinearities

Biophysical computation and spiking models

I am very much still learning how to explain technical stuff in this format, so please bear with me! This post kept getting out of hand so I kept it high-level and moved some details to the footnotes. Let me know what worked and what didn’t 😬.

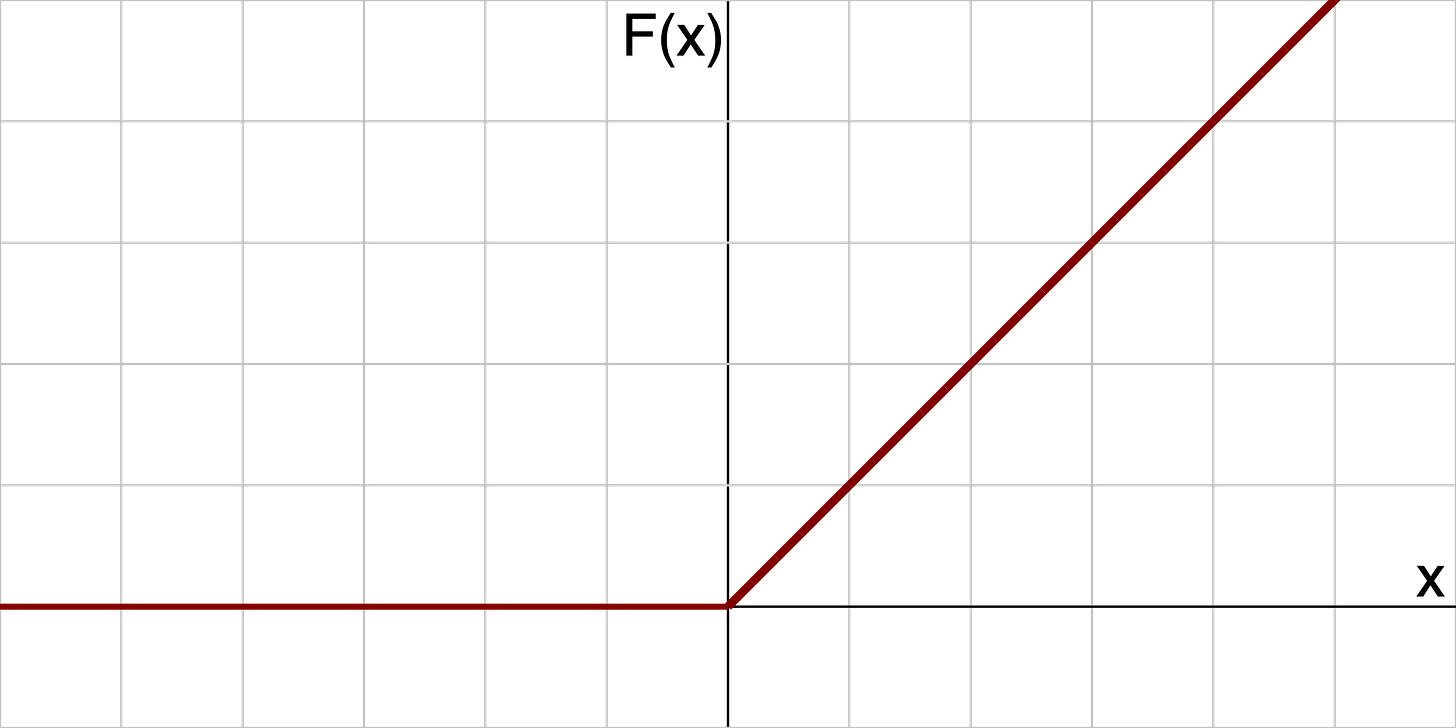
The word “nonlinearity” evokes something specific in the context of artificial neural networks. The classic example is a rectified linear unit (ReLU), which is a function that maps non-positive values to 0 and leaves positive values unchanged¹. The initial motivation for using ReLU was to simulate a firing rate (which cannot be negative) of a neuron given some potentially negative signal². But enforcing biological constraints on deep learning models has not really gotten us anywhere, so the main motivation from machine learning nowadays seems to be that it just… works? (many such cases)

That we use “nonlinear” to refer to these functions reveals that the default operations in artificial neural networks are linear. Linearity is super convenient in engineering and math! But In this post, we’ll see why the brain, starting with its lowest level of computation, cannot be assumed to be linear.

In the last two lectures, we discussed sensory mechanisms that transduce signals into the eventual opening of ion channels. These channels allow the change in voltage, which drive the primary mode of communication in neurons: electrochemical signaling.

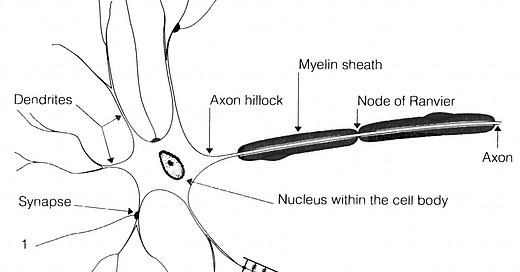
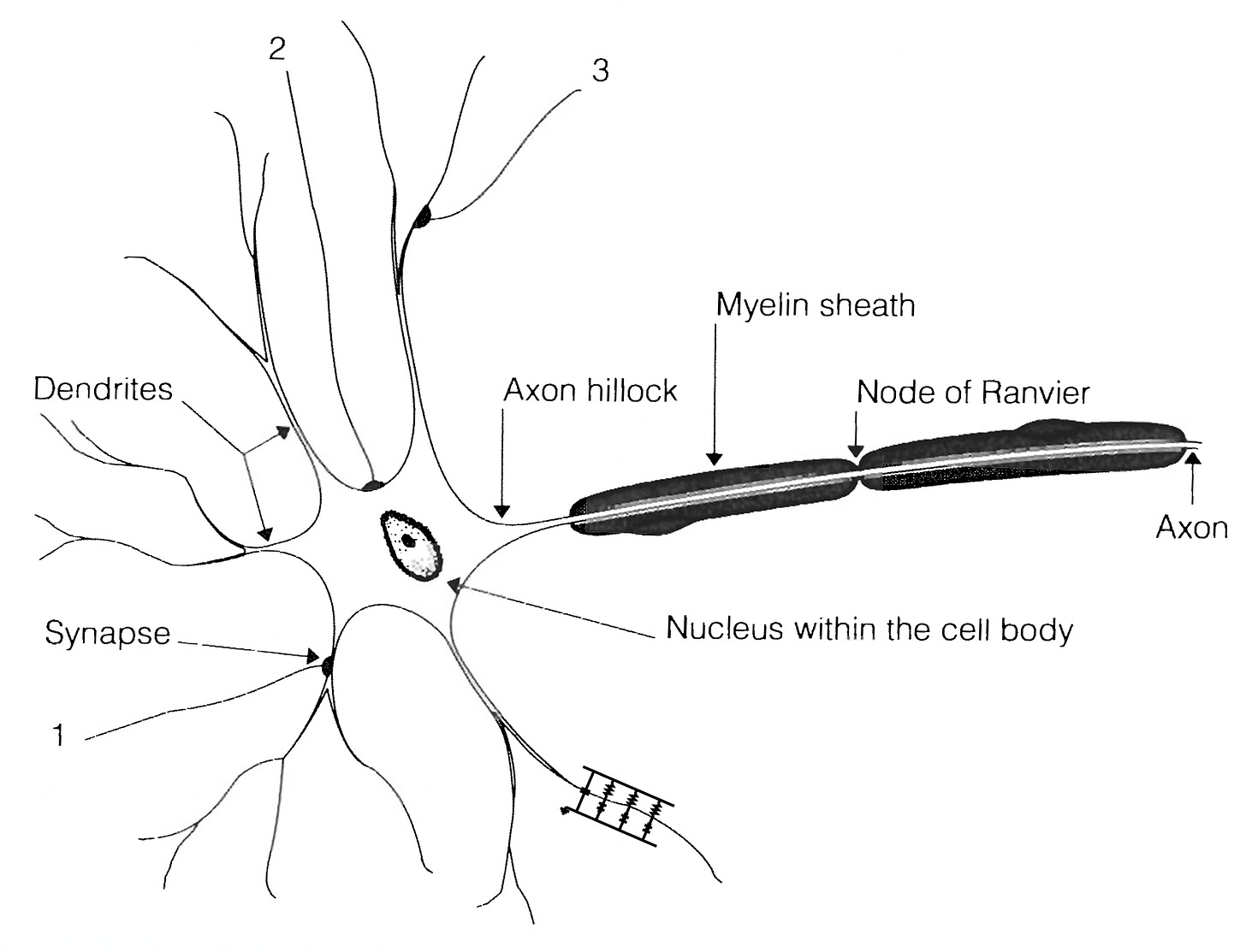
The cell membrane encloses the cell and selectively allows ions to pass through, enabling an electrochemical gradient. We typically think of the dendrites as receiving inputs, on which axons from other cells form synapses and change the voltage inside the dendrites. Current accumulates in the cell body, and when the membrane voltage reaches a certain threshold, an action potential (“spike”) is initiated in the axon hillock and is propagated down the axon³.

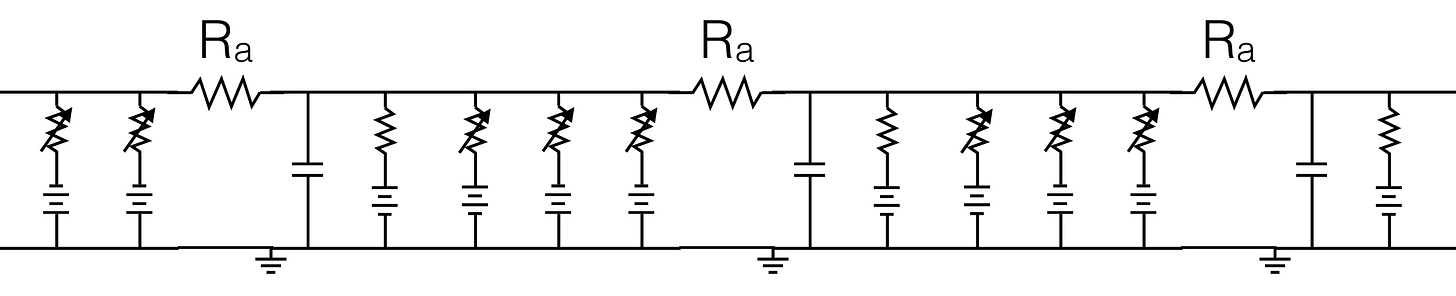
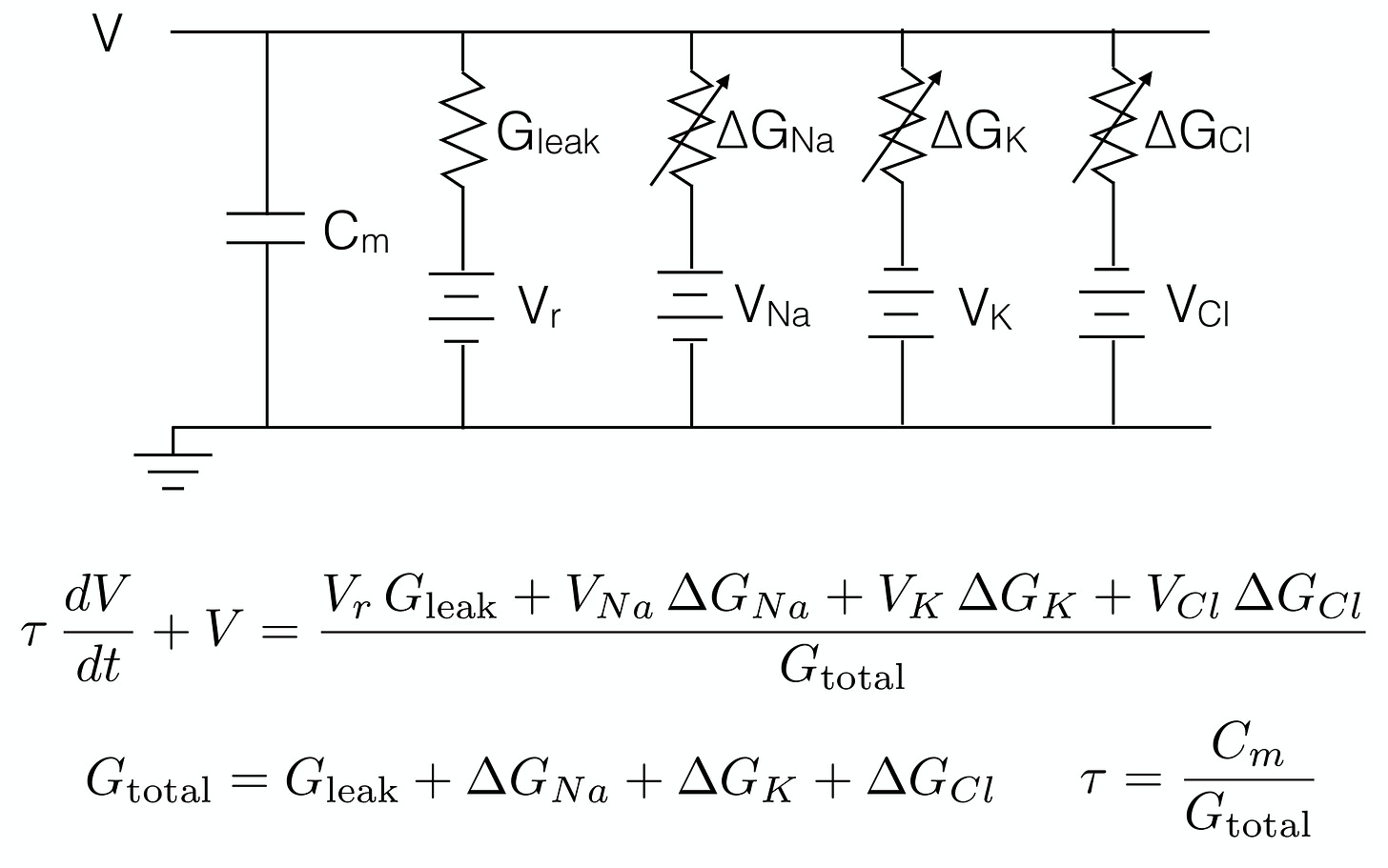
Let’s zoom into that little circuit diagram on the bottom dendrite to look at the membrane equation. You can think of this whole thing as a battery with a difference in potential (voltage) between the inside and outside of the cell caused by a difference in ion concentrations; the ion pumps serve as battery rechargers that maintain the difference⁴.

I’ve put this here for those who want to engage with the circuit diagram and its dynamics, but the main point can be made in words. The ΔGs, or changes in conductance, are input currents (channels opening due to synaptic inputs), which change the membrane potential V (the difference between the inside and outside). I’ll draw your attention to the first equation, which says that in addition to a baseline conductance, both the numerator and denominator are affected by conductance changes⁵. This means that the voltage, which eventually causes spikes, changes nonlinearly with any synaptic input to the cell; the fundamental unit of biophysical computation in the brain is nonlinear.

Shunting inhibition is another nonlinear phenomenon: when only the chlorine channel is open, it does not affect the membrane potential; however, when both chlorine and sodium channels are open simultaneously, the influence of sodium on the membrane potential is inhibited⁶.

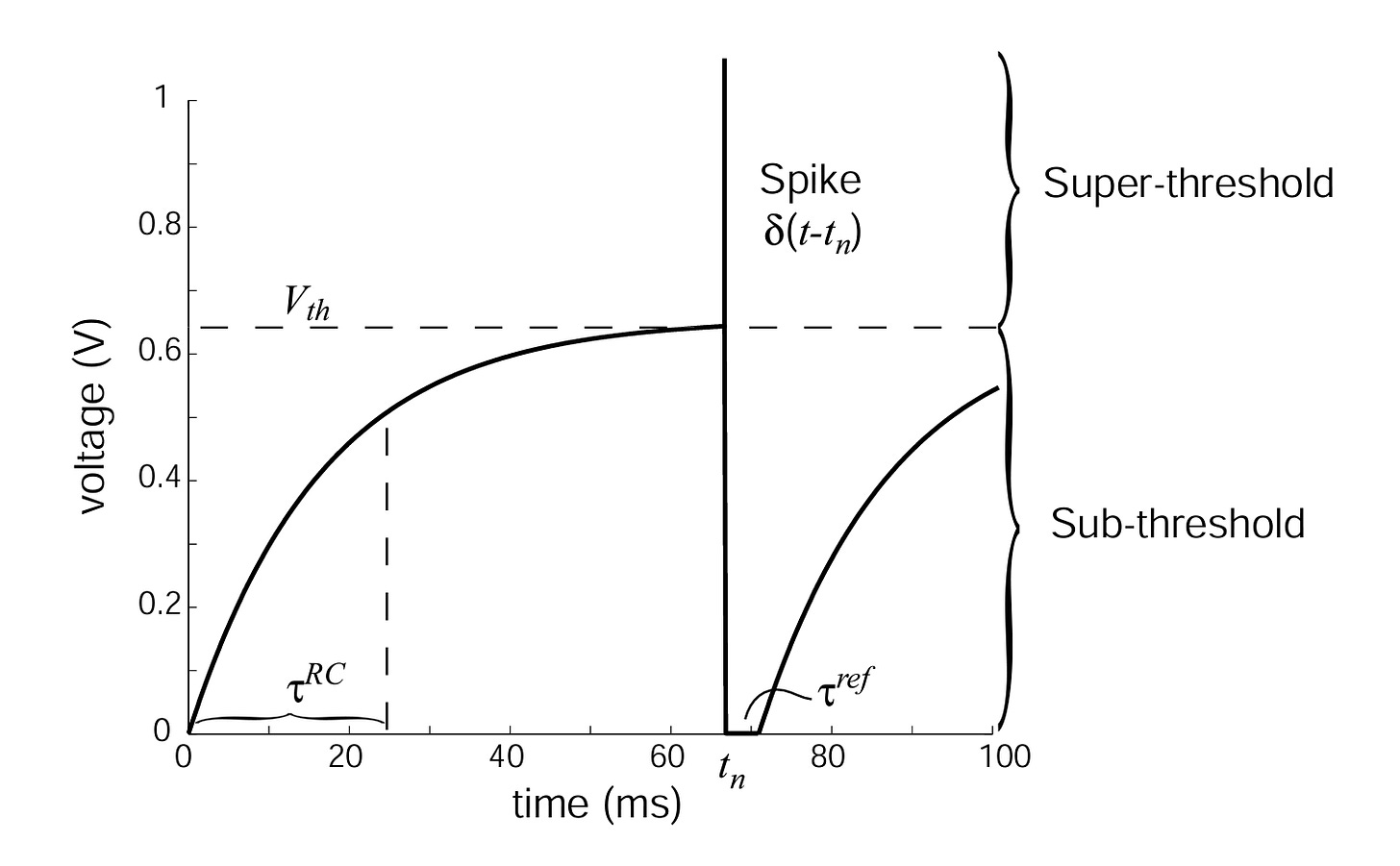
So far, we’ve focused on the membrane potential. But neurons don’t generally convey voltage; they spike. The most basic model of spiking neurons, the leaky integrate-and-fire (LIF) model, is a modification to the membrane equation above, with the addition of a spiking threshold (V_th below), a reset to the resting potential (0 here), and a refractory period (τ^ref). The spikes are the signals sent to other neurons.

LIF with a constant current input. Eliasmith and Anderson 2004.

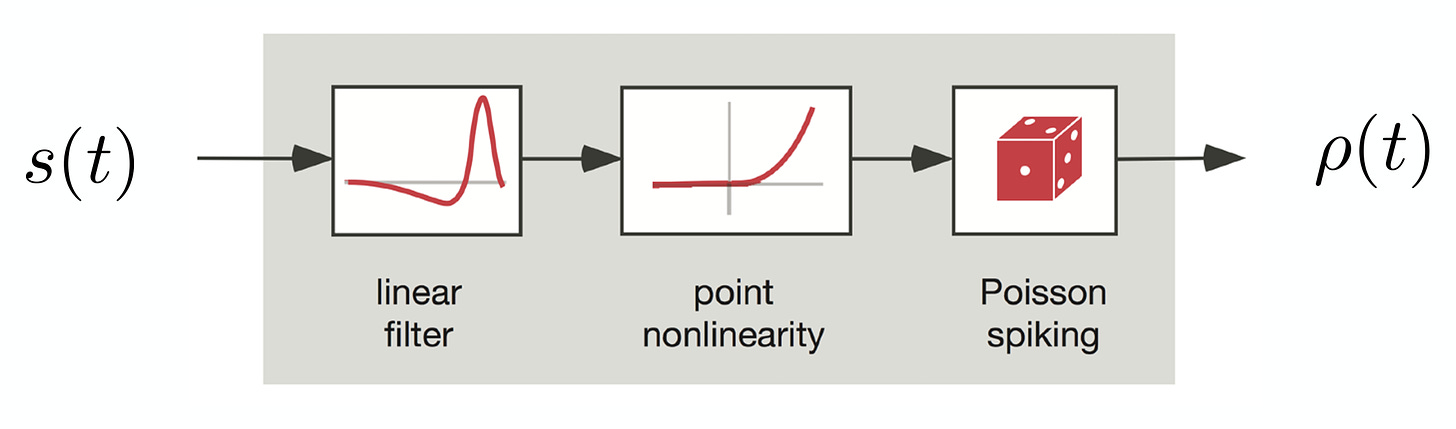
Another way of modeling spikes is with the linear-nonlinear Poisson (LNP) model⁷. A signal is first filtered linearly, then goes through a point nonlinearity, such as ReLU, and is then used as a rate parameter for a Poisson distribution, which gives us spike times. It is nonlinear, and unlike a LIF neuron, the spike times are nondeterministic⁸.

After seeing all this nonlinearity, if you still believe the brain can be well-modeled with only linear operations, or even mostly linear operations, Bruno will throw tomatoes at you 🍅🫵.

We’ve shown a canonical example of biophysical nonlinearity in the brain, and examples of basic spiking neuron models that are also obviously nonlinear. But how do spikes — a compression of an analog to pulsatile signal — convey information? Next lecture, we will talk about encoding and decoding.

1. These point-wise nonlinearities are of course just one example. More generally, we say a function or system F is linear if and only if it satisfies the superposition principle, or both of these properties:

1. Additivity: F(x1 + x2) = F(x1) + F(x2)

2. Homogeneity: a * F(x) = F(a * x) where a is a scalar

For the ReLU, it’s clear that both of these don’t hold for all values, e.g. x1 = 1, x2 = -2 violates additivity and a=-1, x=1 violates homogeneity.

2. Visual Feature Extraction by a Multilayered Network of Analog Threshold Elements, Fukushima 1969.

3. I apologize to the biophysicists as this is an egregious simplification. There are tons of different types of synapses, including dendrite to dendrite, axon to axon, and even reciprocal synapses. Plus, computations don’t just happen in the cell body; dendrites appear to be computing as well. Some dendrites can generate spike-like events to amplify signals over longer distances (another form of nonlinearity). They can even discriminate between temporal sequences (Branco et al. 2010).

4. Some more details: ions are moved across the membrane according to the ion concentration gradient (i.e. they will move from an area of high concentration to low concentration), or by pumps. The circuit diagram shows the top as the outside of the cell, and the bottom as the inside. C_m refers to conductance across the membrane, and each column corresponds to an ion channel that can be modeled with G resistance and V voltage.

5. To visualize, a basic example is f(x) = (1+x)/x.

6. A NAND gate.

7. This is kind of a ridiculous name, similar in flavor to long short-term memory.

8. Are random spike times (a rate code) a good assumption? Maybe? We will talk about time codes versus rate codes in the next post.