I had just read an article by Scott Kirkpatrick on simulated annealing, and I said, “Geoff, we could heat it up, we could heat up the Hopfield network by adding a temperature”, so instead of always going downhill sometimes you pop up and with that, if you slowly cool it we can find the optimal solution… It turns out something magical happens when you heat up a Hopfield network: it becomes capable of learning the weights to a multi-layer network; which is the first time that had been done.
-Terry Sejnowski via The Artificial Intelligence Papers: Original Research Papers With Tutorial Commentaries by James Stone
At the time, the standard way of thinking about cognition was with rule-based symbolic systems. Hinton and Sejnowski’s 1983 paper Optimal Perceptual Inference was unique in approaching perceptual inference using ideas from physical systems. It was the beginning of what would become the Boltzmann machine: a probabilistic, connectionist model of perception. I this post, I’ll attempt to give a brief introduction to the Boltzmann machine.
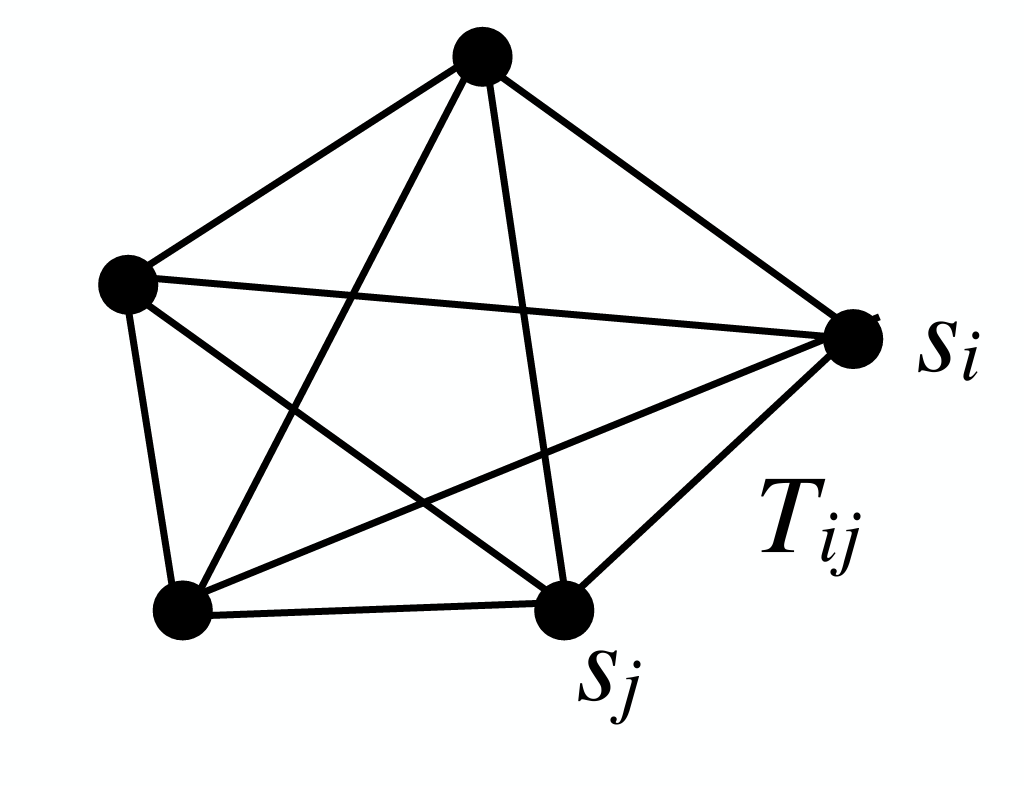
What does it mean to heat up a Hopfield network? Recall that the energy function for a Hopfield network (intro in this post) is
where T is a 2D matrix of fully connected, symmetric weights between units with states sᵢ in {-1, 1}.
To recover a state stored in the weights, we want to travel to a low-energy basin of attraction. Another way you could describe the system is by defining the probability of a state s as
which is called a Boltzmann distribution and depends on the energy and the system’s temperature (1/β). High energy states are low probability and vice versa, as desired. If β is very small (high temperature), then we heat up the Hopfield network for a smoother P(s), and we can move easily between low-energy states. In the other extreme, if β is very large, then P(s) will be sharp peaks at low energy states; in this case, it would be hard to move between them. In the Hopfield network, β is quite high, resulting in a deterministic system. In a Boltzmann machine, β is set such that the dynamics become probabilistic. At a high level, this is a more powerful idea than the original Hopfield network, which is just used for storing exact patterns: the Boltzmann machine allows you to learn a distribution over data, and sample new patterns from the distribution.
Learning and updating
The Hopfield network has a well-defined learning rule to store patterns in weights T. From the Boltzmann distribution, they derived the corresponding learning rule
where < > refers to the average over data points, clamped refers to the states set to some input data, and free refers to the states sampled from P(s). There are two stages of learning: “wake” (clamped) and “sleep” (free). When it’s “awake”, it sees data and updates its weights proportionally to pairwise correlations in data. When it’s “asleep”, it samples from its probability distribution P(s), computes pairwise correlations, and does anti-Hebbian learning (due to the negative sign)1. Intuitively, we want to change the weights such that sampling states from the model’s distribution fits the observed data, i.e. when clamped - free = 0. When the model predicts something different from what’s present in the data, the weights are nudged in the correct direction.
There’s a clear problem with this algorithm, however, and it’s perhaps the reason Boltzmann machines never really took off, at least in the same way deep learning has. Due to the Z normalization term, which contains an integral over all possible states, sampling from P(s) is challenging. The way this is normally done is via Gibbs sampling; as s is a vector, this method samples from a series of conditional probabilities, one dimension at a time, to eventually approximate the joint distribution. Writing out the sampling process, you can rearrange terms to eventually get
which looks almost like the update step for a Hopfield network! But rather than a deterministic thresholding function, we now have a sigmoid function σ that outputs values in [0, 1], indicating a probability of flipping the value, dependent on β and a linear combination of all other values. Remarkably, starting from Gibbs sampling, they arrive at the same flavor of update rule as a deterministic model. Furthermore, just as in a Hopfield network, this is a local learning rule requiring only pairwise connections, and could potentially be implemented in biology.
Hidden units
In the basic setting of the Boltzmann machine, the states serve as both input and output. For a more powerful model that can capture higher order structure (more than just pairwise correlations between units), we add latent “hidden” units (white); visible units are outputs.
For the clamped stage, the hidden states are sampled according to P(sh|sv) (because there is no data to clamp hidden stages to), and for the free stage, both hidden and visible states are sampled from P(s). Although connections are still only pairwise, marginalizing over hidden units effectively lets us capture higher order structure. Suppose you had one hidden unit sh connected to three visible units sv1, sv2, sv3 (not shown above). sh activating would increase the probability that sv1, sv2, sv3 are active together.
Sadly, what’s powerful about the hidden variable model is also what makes it intractable: sampling in the clamped stage becomes very slow due to the hidden units. For each hidden state sample, you need to run a whole Gibbs sampling chain, which must finish before you can sample again. In this form, Boltzmann machines of a nontrivial size are almost impossible to train.
Restricted Boltzmann machine
To address the tractability issue, the Restricted Boltzmann machine (RBM) retains the hidden units, but removes connections between units of the same layer.
The resulting energy function has far fewer dependencies; each hidden unit is only conditioned on a set of visible units and vice versa. This means that we can now sample all hidden units in parallel, without having all the serial dependencies of the original model. This dramatically speeds things up, and allows application to real tasks. For example, Hinton & Salakhutdinov 2006 introduced a “deep” version by stacking RBMs to perform dimensionality reduction via autoencoding. To initialize the network parameters, they trained several small networks separately and connected the outputs of one layer to the inputs of the next. After this pre-training, they used backpropagation to finish fine-tuning the network, and could also perform classification using the pre-trained network.
Don’t listen to your advisor?
Later, going against Hinton (their advisor)2, Alex Krizhevsky and Ilya Sutskever dropped the pre-training part and just did backprop in AlexNet. It worked better than anything else and led to deep learning as we know it today.
The messaging of Hinton’s recent Nobel Prize seemed to suggest that success in deep learning came about as a result of the RBM. In reality, it’s more like it happened in spite of the RBM. This is not to detract from the scientific significance of the RBM or Hinton and Sejnowski’s work, and it may be that the great breakthroughs of the RBM for AI are still yet to come. But the morals of the story are perhaps that 1) great discoveries often result from disobedience, and 2) scientific innovation does not always translate to real impact.
I skipped over details for the RBM, but see Hinton and Sejnowski’s chapter in Parallel Distributed Processing. In the next post, we’ll cover the final main topic of the course: computing with high-dimensional vectors.