Computing in high dimensions
Featuring a dip back into 𝖞𝖊 𝖔𝖑𝖉𝖊 AI history
Current machine learning relies on manipulation of high-dimensional vectors. The classic Word2vec represents a word as a vector and associates semantic similarity with distance in a vector space. Transformers in large language models (LLMs) convert words to large vectors and perform operations like inner products, concatenation, and thresholding on them. These approaches are in the spirit of the connectionist AI philosophy, inspired by the machinery of neurons inside the brain and training a model to learn from the statistics of data. One weakness of connectionism is that it is unclear whether it can do things we consider important for cognition, such as bind variables, represent relationships between concepts, and compose expressions.
The contrasting old-school approach, symbolic AI, uses high-level logical and human-readable symbols as the basis for intelligence, and explicitly represents data structures (graphs, trees, etc.), variables, and relationships, as in computer programming. It’s a powerful framework, but is not designed to learn from and adapt to the world, and has fallen out of fashion in these data-powered times.
This is a standard narrative of connectionist vs. symbolic AI1, but there’s another more neuroscience-y weakness of connectionism to acknowledge. It was inspired by single-unit recordings in the brain and the idea that recording from individual cells conveys important information about neural computation, borne out of technological limitations that only allowed us to record from one neuron at a time. But the single cell angle is not the only way to think about computation in a network; recorded activity from one neuron is certainly not incorrect, but it does not tell us the whole story2, especially in the highly recurrent circuits of the brain. We also now have technology, such as Neuropixels, that allows us to record from hundreds or thousands of neurons simultaneously.
An approach that attempts to address some of the limitations in both connectionist and symbolic AI is Hyperdimensional computing (HDC, Kanerva 1997)3. In HDC, the fundamental unit is the activity of a population of units, in the form of a vector. It is not just a convenient representation; it is a different computational framework, where the primitives are vectors. Looking at a single value in the vector may tell you something, but it conceals the power of the system. HDC allows us to use the symbolic tools of data structures and logical operators while retaining some desired connectionist properties. We’ll demonstrate this through some examples.
HDC algebra
HDC defines an algebra over vectors, where the values of a vector could be binary, real, complex, etc. Given a concept, like a word, a color, or an image, we assign it a random high-dimensional vector. The main operations, which maintain the same dimensionality, are (random vectors in bold)
Bundling: u = a + b + c, where + is element-wise addition. This combines a set of discrete items into one vector
Binding (variable assignment or key-value pairing): d = k ⊙ v, where ⊙ is e.g. element-wise multiplication (Hadamard)
Permutation (ordering vectors): s = a + ρb + ρ2c, where ρ is a constant
It is also easy to compare similarity between vectors, and a simple example is taking the inner product. u • a would have a nonzero inner product, whereas u • d would likely be close to 0.
The randomness and high dimensionality here are key: if vectors are orthogonal or close to orthogonal, information contained in u, d, and s can easily be decoded, queried, and used to perform reasoning without a serial search through the set. The higher the dimension, the more likely it is that random vectors are orthogonal, and the less likely it is that there will be cross-talk between vectors4.
Although it’s not without limitations, here’s a high-level summary of some advantages of HDC.

I have been vague about what querying and reasoning mean so far, but we’ll try to concretize these in the following examples.
Variable binding and language
Tony Plate developed Holographic Reduced Representations (HRR) as a graduate student with Geoff Hinton. At the time, they were interested in getting connectionist systems to do symbolic reasoning. HRR was inspired by Paul Smolensky’s tensor product variable binding (1990), but instead of keeping the expanded dimensionality, compressed the tensor into a lower dimension using circular convolution.
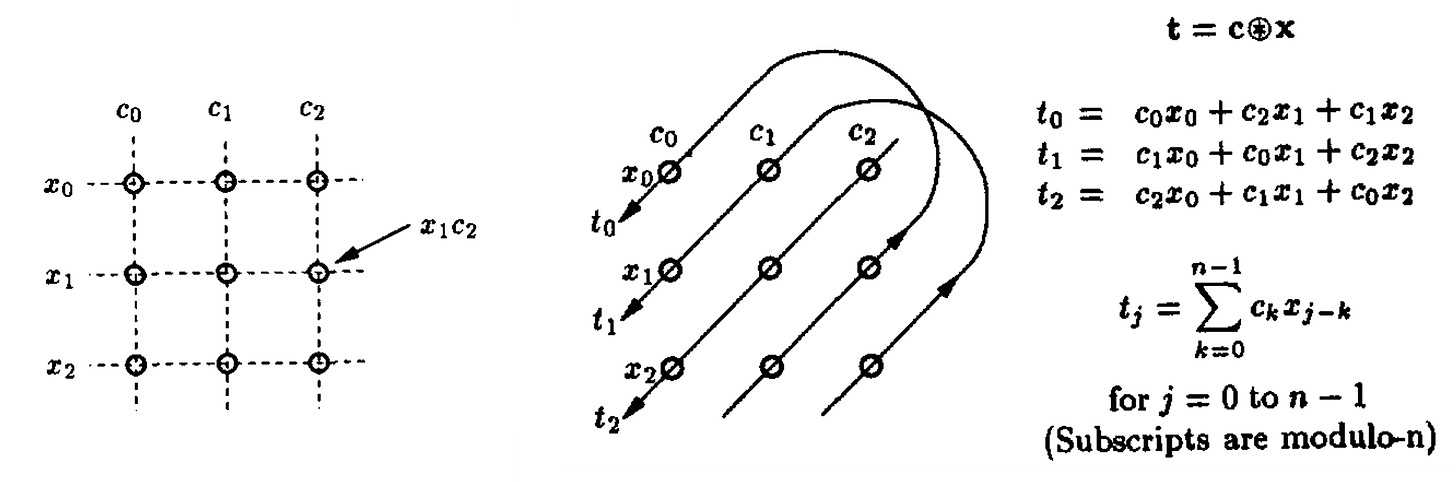
Plate’s method allows storage of lots of information within one N-dimensional vector, provided N is large enough. Querying the vector is also straightforward. Suppose we want to represent a word x that has part of speech c. We bind via circular convolution (⊛): t = c ⊛ x, and unbind using the correlation operator (⊜5) to get back an estimation of the word x ≈ c ⊜ t. We can compose two bound variables: t = c1 ⊛ x1 + c2 ⊛ x2 and get back an estimation of x1 ≈ c1 ⊜ t, e.g. if we wanted to get the word with part of speech c1 in the phrase t.
Here’s a more concrete example on language. We can represent parts of speech, roles, grammatical structures, and not just superpositions of words, but recursive superposition of words and their roles. For example, to represent the sentence “Spot bit Jane, causing Jane to flee from Spot”, you could construct a highly-structured vector that assigns meaning to each word
agt refers to the agent performing the verb, < > denote unit normalization, and each variable in bold is a random high-dimensional vector (say length=2048). You can query P for who’s doing the biting or fleeing, for example, and also compare the similarity between P and other sentences created using the same vectors. Surprisingly, something as simple as the inner product works quite well as a first-pass similarity measure, as shown in Plate’s thesis (1994), chapter 6.
Although this is a simple example compared to scale of what LLMs are doing now, you can see how easily recursive structure, such as a parse tree, can be stored and accessed efficiently in HDC.
Analogical reasoning
Researchers like Douglas Hofstadter and Melanie Mitchell have long been studying analogical reasoning as a key component of intelligence and reasoning6. The Abstraction and Reasoning Challenge (ARC) and variants have recently gotten a lot of attention7 for being hard to solve with LLMs. Although beating a benchmark is not equivalent to solving a problem, we have not yet saturated these benchmarks.
One basic example of analogical reasoning in HDC comes from Pentti Kanerva (2010). How would we answer a question like What is the dollar of Mexico?
For the variable names, we have Name, Capital, and Monetary unit of the country. For USA, those variables are bound to the values Us, Dc, and $, respectively. The binding operator is * here.
We can bind the two vectors representing the countries
which can also be written as
This can be derived from distributivity and the fact that Pentti uses vectors and a * such that A*(A*X) = X. The noise comes from the fact that all other terms should be approximately orthogonal and result in very small values. To answer the original question, we ask what in Mexico corresponds to $ in USA? and unbind $ with Pair:
to get the correct answer, P for Peso. This is all made possible by this simple algebra in high-dimensional space. This is of course a basic analogy, but we can represent much more complex ones with negligible extra computational cost.
At this point, you might be scratching your head. Of all the increasingly disconnected-from-reality topics we’ve covered in the past few posts, this is by far the most abstract. Despite its simple operations, it’s difficult to wrap your head around the idea of HDC as a distinct computational framework. But even more abstract still is its connection to the brain.
The short answer is that the motivation for HDC comes more from cognitive science and AI than neuroscience. Binding, bundling, and permutation operations are first principles-driven, and not from biology (though perceptrons didn’t come from biology either!). But there is importance in stepping away from neurobiological plausibility (the theoretical neuroscientist’s frenemy) and thinking about what types of computations would be required to perform cognitive reasoning. We’re exploring this framework now, with the ultimate goal of mapping it onto actual implementations in brain circuits. This mindset is not unique to HDC; this is more generally why theory is important8!
HDC is relatively under-explored, but we’re excited to see where it goes in the coming years. Chris Kymn’s recent NeurIPS paper very elegantly uses approaches from HDC and attractor networks to model hippocampus and entorhinal cortex. For a recent review of HDC applications, see Kleyko et al. 2023. And here’s a nice 2023 feature of Bruno and Pentti in Quanta Magazine.
I am absolutely not an expert on AI history/philosophy, so you should read all the other stuff out there. E.g. Maxim Raginsky’s recent post has more in-depth analysis of LLM reasoning in the connectionist-symbolic framework.
This again recalls the parable of the blind men and the elephant that I referenced in the first lecture post.
It was also introduced by many around the same time using different names: Holographic Reduced Representations (Plate 1994) and Vector Symbolic Architectures (Gayler, late 1990s).
For non-hand-wavey versions of these statements, see Thomas et al. 2021.
The symbol should be a # inside a circle but I can’t find the right character.







